BTree
B树
阶: B树中所有结点的孩子结点个数的最大值即为阶
性质:
N个关键字,则有N+1个指针
M个分支,则有M-1个关键字
除根结点之外,其他结点至少有 [M/2向上取整] 个孩子结点
3.1 分支的范围 属于 [M/2向上取整] ~ M
3.2 关键字范围 属于 [M/2向上取整]-1 ~ M-1
若根结点不为叶子结点,则根结点至少有2个孩子结点
所有叶子结点都在同一层,即平衡因子为0
B Tree 插入(例)
假设该B Tree的阶为5
根据以上性质可以得出 -» 分支的范围为[3,5]// 关键字的范围为[2,4]
首先,依次插入{12, 18, 33,39,50}

这时,发现关键字个数超出了关键字的范围,应当向上分裂。
PS:向上分裂 -» 中值向上一层提出
故应所得
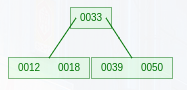
插入其他数值也应当依据该原理。
ⸯⸯⸯⸯⸯⸯ
插入其他数值的过程在此不再赘述
最终得图
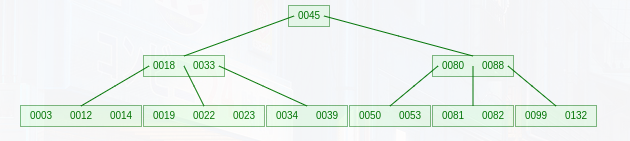
B Tree 删除(例)
以上图为基础
非终端结点的删除
用其直接前驱或直接后继代替即可。
例如删除 ‘33’
可以直接用其直接前驱代替,33的直接前驱为23(直接前驱即该值左指针部分右下角的值)
也可以用直接后继代替,33的直接后继为34(直接后继即为该值右指针部分左下角的值)
但在此若用直接后继代替,则会发现其直接后继所属块关键字数量不在范围内,故需用到终端结点删除的知识,下文中会介绍到,故此处用其直接前驱直接代替 (使用该方法时切记注意终端结点关键字数量是否在范围内!)
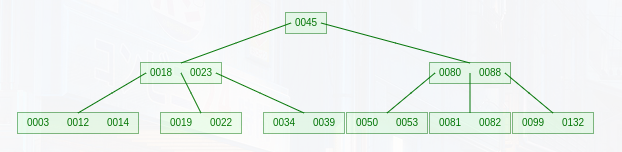
终端结点的删除
若删除后,结点的关键字数量仍在范围内,则不进行操作
若删除后,其范围低于下限
1. 右兄弟够借 -» “逆时针”操作 (逆时针操作:用后继的后继代替后继位置,用后继代替该值,删除后继的后继位置)
2. 左兄弟够借 -» “顺时针”操作 (顺时针操作:用前驱的前驱代替前驱位置,用前驱代替该值,删除前驱的前驱位置)
3. 左右兄弟都不够借 -» 借双亲结点,删除该结点,合并兄弟结点(可能需要对双亲结点进行该操作)
例如删除‘81’
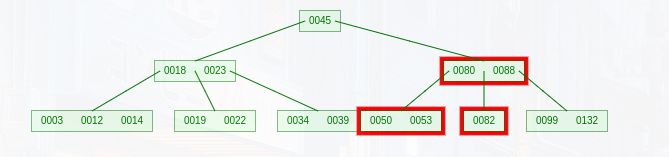
此时82块不在范围内,向左兄弟借,不够借;向右兄弟借,不够借;则向双亲结点借,之后删除该值,合并兄弟,得到

此时88块不在范围内,左兄弟不够借,则向双亲结点借,同上一步,得图

例如删除‘99’
应当向左兄弟借,进行顺时针操作,得图

例如删除‘14’
删除后,关键字数量仍在范围内,不进行操作,故得

总结
B树的插入
1. 在插入完成后,若关键字数量仍在范围,不进行操作
2. 如果关键字超出范围,则进行向上分裂操作
B树的删除
1 |
|


